先日、ツイッター上で「リスクが高いとリターンはさがるの?」「リスクはリターンを蝕むってどういうこと?」という話題で議論になりました。
インデックス投資ブロガーの先人のみなさんの記事のおかげで、概念的なところは理解できているつもりでいたのですが、いざその論理的根拠を説明しようと思うと、これがなかなか難しい。
この議論をきっかけに、改めて、
- リスクはリターンを蝕むということはどういうことなのか
- リスクとリターンと複利の関係
について調べてみたいと思うようになりました。
それはすでに先人が歩み開拓した道
リスクとリターンと複利の関係に関しては、投資信託のブログ|ファンドの海のイーノ・ジュンイチさんの連載記事リスク資産の複利確率 が鉄板です。
そして、その連載を通して得られた知見をすべてつぎこんだ、投資家向けのツール長期投資予想/アセットアロケーション分析を公開してくださっています。
このツールは、まさに、アセットアロケーション分析・資産設計シミュレーションの最終兵器といってもよいものです。
アセットアロケーションを入力すると、全体の期待リターン、リスク、長期間投資後の運用結果の分布、確率毎の運用結果の目安などが一発で、しかも、きれいなグラフで表示されます。
アセットクラス間の相関係数や、計算期間などがカスタマイズできるなどかゆいところにも手がとどく親切設計です。
そう、すでに答えは全て、イーノさんの記事のなかにあるのです。
その足跡をあらためてたどる
そこで、今回、イーノさんとその読者のみなさんが当時歩まれた足跡をあらためてたどることにより、自分自身の理解を深めることにしました。
この記事は、その足跡をあらためてたどる過程で感じたこと、理解したことのメモです。イーノさんの記事を読み進めるうえで、少しでもお役にたてるとうれしいです。
すばらしい記事を残してくださったイーノ・ジュンイチさん、議論に加わっておられた先人にみなさまに感謝感謝です。
この記事は、一番重要な数式に一気通貫ワンストップでたどり着けるようにしたため、少々長くなっています。たまに数式も出てきます。腰を落ち着けて読めるときに読むこと推奨です…。
リスクはリターンの敵であることがよくわかるグラフ
最初から結論「リスクはリターンの敵」、「リスクはリターンを蝕む」がよくわかるグラフをご紹介します。
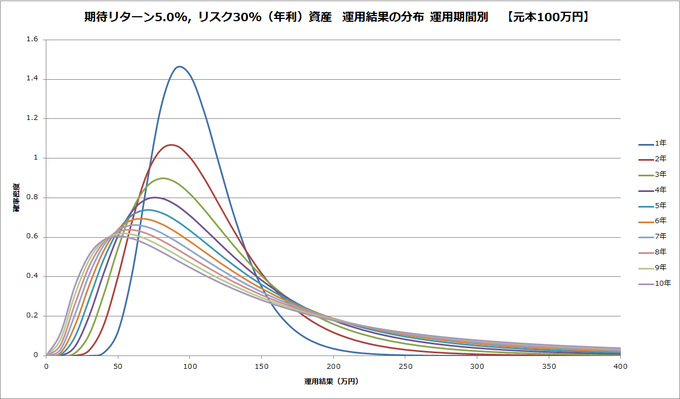
以下のグラフはいずれも、元本100万円を、ある期待リターン・リスクのある資産で、一定期間運用した結果、最終的にいくらになっているか、の分布、を表現しています。横軸が運用後の金額、縦軸が頻度(厳密には確率密度=連続な度数分布)です。
まずは、期待リターン5%、リスク30%(いずれも年率)の資産を1, 2,…,10年と運用していった場合の分布です。
運用期間が長くなるにつれ、グラフの山(最頻値=最もありそうな)が左側、すなわち、資産が少なくなる方向に移動しています。
期待リターン5%、リスク30%の資産は運用期間が長くなれば長くなるほど、最もありそうな最終金額が減っていくということです。時間の経過とともに、まさに、リスクがリターンを蝕んでいる様子が見てとれます。
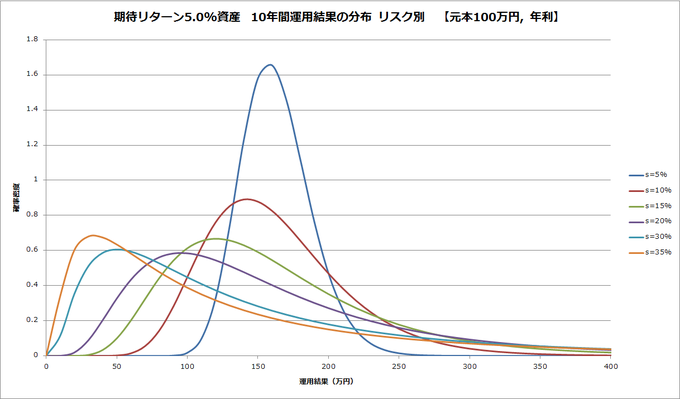
次に、期待リターンはいずれも5%で、リスクが5%, 10%, 15%,…,30%, 35%と異なる資産を10年間運用した場合の分布です。
リスクが高くなるにつれ、やはりグラフの山が左に移動していきます。
最初に、最終結果であるグラフを出してしまいましたが、このグラフにたどりつくまで長く険しい道のりがあります。この道を歩んでいたのがイーノさんの連載記事なのです。
以降の節では、イーノさんが歩み結論に到達された道をあらたためてたどっていくうえで、私がひっかかった点、ポイントだと感じた点を、トピックス毎にご紹介していきます。
正規分布するのは一定期間後のリターンではなく、連続複利収益率だった
投資や資産形成の書籍には、「リターンは正規分布する」、「リスクをσ(年率)とすれば、1年後に期待リターン±σにおさまる確率は68%、期待リターン±2σにおさまる確率は95%」といったことが書いてあります。
ただし金融工学ではこれは厳密には正しくなく、正確には「連続複利収益率が正規分布する」とされているとのことです。
「え!よく本に書いてあった、1年後に期待リターン±σにおさまる確率は68%というのは間違いだったの?」と心配されている方がいるかもしれません。
ご安心ください。
短い期間でみると「一定期間後のリターンが正規分布する」も「連続複利収益率が正規分布する」も結果はほとんど同じになります。十分近似します。
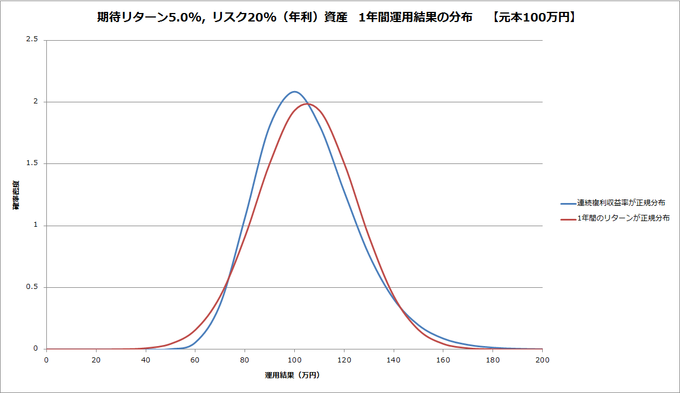
それを確認するために描いたのが以下のグラフです。元本100万円を期待リターン5%、リスク20%の資産を1年間運用した場合の結果の分布を、二つの考え方に基づき描いたものです。
グラフの形は「連続複利収益率が正規分布する」の山が少し左によっていますがほぼ似たような形です。
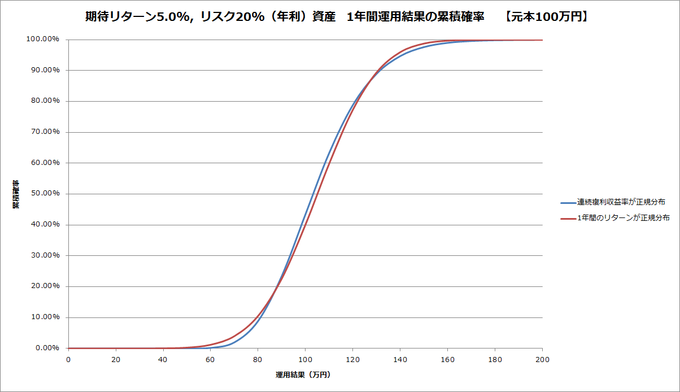
下のグラフは、それぞれの累積確率を描いたものです。累積確率というのは、上の運用結果の縦軸の値(確率密度)を下から累積していったものです。グラフ上の点の横軸の値をX、縦軸の値をYとすると、運用結果がX万円以上になる確率は(100-Y)%という見方をします。
これを見ると、二つの線がほぼ同じ、つまり、金額と確率の対応関係がほぼ同じことがわかります。
対象期間が長くなる場合は、ずれが大きくなって近似とはいえなくなります。先の10年間の運用結果の分布をしめすグラフの形はどうみても左右対象の釣鐘ではないですよね。
この結論にいたるまでの道のりは
- リスク資産の複利確率(7)~ 食い違う計算結果とシミュレーション結果の「謎」
- リスク資産の複利確率(8)~ 謎を解くカギは「B方式」にあるらしい
- リスク資産の複利確率(9)~収益率の変化をシミュレーションするという
- リスク資産の複利確率(10)~どうして収益率を足しているのだろう?
の記事が詳しいです。「一定期間後のリターンが正規分布する」という前提でシミュレーションしたところどうも結果がおかしい、なぜだ?というところから、「連続複利収益率が正規分布する」に辿りつくまでの過程がドラマチックに書かれています。リアルタイムで読みたかった…。
連続複利収益率とは
連続複利収益率とはなにか。ひとことでいうと「一瞬の収益率」。複利で考えた際、保持している瞬間瞬間で収益をあげているという考えのもとに計算できる「一瞬の収益率」です。
株式など収益を生む資産は、半年おき、1年おきに(離散的に、非連続的に)ドンと収益が発生するわけではなく、1年、1ヶ月、1日、1時間、1分、1秒、0.1秒、0.01秒など極限まで細かくした瞬間瞬間で発生しているという考えに基づいています。
リスクのある資産の場合、この、極限まで細かくした「一瞬の収益率」が正規分布するというわけです。
- 収益率は持っている瞬間瞬間で変化するもの
- その瞬間瞬間の収益率の変化が正規分布する=ある値を中心してばらける
の二つが頭の中でつながった瞬間、「なるほど」とすっと腹におちて、爽快でした。
連続複利についての説明と、公式については
- リスク資産の複利確率(11)~連続複利とは? 無限に連続する複利の金利を求める
- リスク資産の複利確率(12)~連続複利を計算してみた
- リスク資産の複利確率(13)~連続複利の世界では掛け算が足し算になる!
- リスク資産の複利確率(14)~ 収益率を連続複利だと想定したシミュレーション
の記事が詳しいです。
連続複利収益率の求め方 式の導出
連続複利収益率はどう求めるのか。式の導出が省かれていたこともあり、私は一度ひっかかったので、自分なりに理解した内容をご紹介します。
元本![]() 円を預けた場合、1年後には
円を預けた場合、1年後には![]() 円になる
円になる![]() 年複利の金利(年利)
年複利の金利(年利)![]() の定期預金について考えるとわかりやすいです。
の定期預金について考えるとわかりやすいです。![]() なら、1ヶ月複利です。
なら、1ヶ月複利です。
この定期預金を一期間、つまり![]() 年預けた後の金額は
年預けた後の金額は![]() です。
です。![]() になっているのは
になっているのは![]() は年利換算ですが、一期間は
は年利換算ですが、一期間は![]() 年なので
年なので![]() を
を![]() で割っています。
で割っています。
これをさらに一期間、合計二期間あずけたら![]() になります。
になります。
これをくりかえして、つごう![]() 期間=1年間預けたら
期間=1年間預けたら![]() になり、これが
になり、これが![]() に等しくなるわけです。
に等しくなるわけです。
ここで、一期間を極限まで細かくする、つまり、![]() を限りなく大きくしたら
を限りなく大きくしたら![]() がどうなるかを考えます。
がどうなるかを考えます。
![]() を限りなく大きくする…、むかし数学の授業でやりましたね…。
を限りなく大きくする…、むかし数学の授業でやりましたね…。
![]() みたいなやつです。私もがんばって思いだしましたよ。
みたいなやつです。私もがんばって思いだしましたよ。
![]()
を
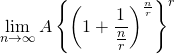
と変形します。
理由は自然対数(ネイピア数)![]() の定義
の定義
![]()
の形にもっていきたいだけです。考えてはいけません。そういうものなんです。
![]() とおくと
とおくと![]() で
で![]() なので
なので
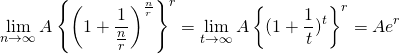
となります。考えてはいけません。そういうものなんです。
つまり
![]()
であり、両辺を![]() で割り、底が
で割り、底が![]() の対数を取ると
の対数を取ると
![]()
になります。
この![]() が、一瞬の収益率(定期預金の場合は金利)、すなわち、連続複利収益率(定期預金の場合は金利)です。
が、一瞬の収益率(定期預金の場合は金利)、すなわち、連続複利収益率(定期預金の場合は金利)です。
説明では![]() を年利としたので、このときの
を年利としたので、このときの![]() は「年利
は「年利![]() %の、連続複利(年利)」になります。
%の、連続複利(年利)」になります。
![]() を1ヶ月の金利(収益率)にすれば
を1ヶ月の金利(収益率)にすれば![]() は対応する連続複利(1ヶ月)になるわけです。
は対応する連続複利(1ヶ月)になるわけです。
連続複利収益率が正規分布だといろいろつじつまがあう
「連続複利収益率が正規分布する」とすることにより説明がつきやすくなること、納得しやすくなることがあります。
株式を持っていたとき、それが紙くずになる可能性はありますが、追い打ちでお金を要求される事態にはなりませんよね。
しかし、正規分布は、左右対象の釣鐘の形でマイナス方向、プラス方向の方法に無限に広がっています。確率は極めて低いとしても-4σ、-5σだって理論上はありえます。例えば、期待リターン5%、リスク30%の資産で-4σの事象が発生した場合、保有資産がマイナスになる計算になります。
他方、「連続複利収益率が正規分布する」とした場合、最終的な保有資産の分布は対数正規分布に従うことになり、原理的に0以下(ピッタリの0を含むそれより小さい値)にはならないのです。
なお
などで触れられているとおり、「収益率の変化が正規分布する」では説明しきれないファット・テールと呼ばれる考え方もあるようです。
ただ、この記事でも、イーノさんの記事同様、ファット・テールについてはまだ手に負える状態ではないので、あえて考慮せず「連続複利収益率が正規分布する」の前提で進めることにします。
連続複利収益率をつかうと複数期間の計算が楽になる
連続複利収益率![]() の概念を使うと、複利を簡単に扱えるようになります。
の概念を使うと、複利を簡単に扱えるようになります。
ここでも、リスクのない年利![]() %の定期預金で考えます。すると、先に見たように1年後の金額は
%の定期預金で考えます。すると、先に見たように1年後の金額は
![]()
と指数で表現することができるようになります。
指数は、かけ算を足し算にしてしまうための道具です。複利は、かけ算の繰り返しですから、指数を使うことにより、複利を足し算で扱えるようになるのです。
どういうことなのか見ていきます。
1年後の金額は![]() なので2年後の金額は
なので2年後の金額は![]() です。これを繰り返していくと、
です。これを繰り返していくと、![]() 年後の金額は
年後の金額は![]() になります。
になります。
同じことを連続複利収益率で考えると1年後の金額は![]() 、なので2年後の金額は
、なので2年後の金額は![]() です。これを繰り返していくと、
です。これを繰り返していくと、![]() 年後の金額は
年後の金額は![]() になります。
になります。
![]() の
の![]() 乗が
乗が![]() の
の![]() 倍になったのが、かけ算が足し算になっている部分です。
倍になったのが、かけ算が足し算になっている部分です。
リスクのない定期預金の例だけでかんがえると、あまりありがたみが感じられないかもしれませんがリスク(ブレ)とそれに伴なう結果の分布を考えはじめるとパーッと世界が広がっていきます。
連続複利収益率が正規分布するということ
連続複利収益率について把握できたところで「連続複利収益率が正規分布する」が意味することを考えてみます。
連続複利収益率を![]() とすると、リスクはこの
とすると、リスクはこの![]() の変動によりもたらされ、その
の変動によりもたらされ、その![]() の変動が正規分布に従うということです。
の変動が正規分布に従うということです。
つまり、![]() の分布の平均を
の分布の平均を![]() 、標準偏差を
、標準偏差を![]() (分散は
(分散は![]() )とすると、
)とすると、![]() は正規分布
は正規分布![]() に従う確率変数であるということです。
に従う確率変数であるということです。
こう書くととても難しく感じるかもしれませんが、リスク資産の毎年のリターンは変動するけど、それは連続複利収益率![]() が正規分布
が正規分布![]() に従って変動した結果である、と考えるといろいろ簡単に考えられる、ということです。
に従って変動した結果である、と考えるといろいろ簡単に考えられる、ということです。
ここで、リスク資産の期待リターン![]() とリスク=標準偏差
とリスク=標準偏差![]() (分散は
(分散は![]() )と、
)と、![]() の正規分布のパラメタ
の正規分布のパラメタ![]() の関係を見てみます。ここの関係を理解するのが少々ややこしいのです。イーノさんの記事でも、この部分が難しく苦労したとあり、数式の導出が省かれているところでもあります。
の関係を見てみます。ここの関係を理解するのが少々ややこしいのです。イーノさんの記事でも、この部分が難しく苦労したとあり、数式の導出が省かれているところでもあります。
考え方のポイントは
 が正規分布
が正規分布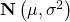 に従って変動した結果=運用結果である資産額の分布は対数正規分布であること
に従って変動した結果=運用結果である資産額の分布は対数正規分布であること- その分布は、平均が
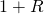 で標準偏差が
で標準偏差が (分散は
(分散は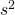 )であるということ。
)であるということ。
です。
対数正規分布 指数の世界と現実の世界を結ぶ道具
ここで、対数正規分布という、多くの方にとって聞き慣れない言葉が出てきました。これが指数の世界から現実の世界へ戻ってくるための道具です。
対数正規分布は「確率変数の対数をとった値が正規分布に従うような分布を対数正規分布という」と定義されます。
![]()
の式を思いだしてください(今度はリスク資産での運用を考えているので、言葉を変えます)。
元本![]() 円を、年利期待リターン
円を、年利期待リターン![]() で1年運用した後の金額です。リスク資産ですから、この1年運用後の金額は変動するということ。つまり
で1年運用した後の金額です。リスク資産ですから、この1年運用後の金額は変動するということ。つまり![]() が確率によって変わる値、確率変数です。
が確率によって変わる値、確率変数です。
この確率変数![]() の対数を取ると
の対数を取ると![]() になります。
になります。
あれ?どこかで見たことがありますね…そう。連続複利収益率![]() を求めるときに出てきました。
を求めるときに出てきました。
![]()
です。
つまり、![]() は確率変数
は確率変数![]() の対数であり、しかも正規分布
の対数であり、しかも正規分布![]() に従うのです。
に従うのです。
ここまでわかったことの合わせ技で、![]() は正規分布
は正規分布![]() に従い、
に従い、![]() は対数正規分布
は対数正規分布![]() に従うということがわかります。
に従うということがわかります。
これらを組み合わせると1年後の運用結果の分布は
![]()
となることがわかります。
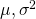 を
を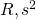 で表現する式の導出
で表現する式の導出
また対数正規分布![]() に従う確率変数
に従う確率変数![]() の平均
の平均![]() が
が
![]()
であること。
分散![]() が
が
![]()
であること。
![]() は対数正規分布
は対数正規分布![]() に従い、結果の平均が
に従い、結果の平均が![]() 、標準偏差が
、標準偏差が![]() (分散は
(分散は![]() )であること。
)であること。
これら三点を利用すると、リスク資産の期待リターン![]() ・リスク=標準偏差
・リスク=標準偏差![]() (分散は
(分散は![]() )と、
)と、![]() の正規分布のパラメタ
の正規分布のパラメタ![]() を結びつけることができるようになります。
を結びつけることができるようになります。
![]() を
を![]() で表現することを目指すわけです。
で表現することを目指すわけです。
これができると、普段よく目にする年率の期待リターン・リスクから、「連続複利収益率が正規分布する」の考えに基づいた運用結果の分布を求めることができるようになります。
対数正規分布![]() に従う確率変数
に従う確率変数![]() の平均
の平均![]() 、分散
、分散![]() の特徴から
の特徴から
![]()
![]()
です。
![]() の両辺を2乗すると
の両辺を2乗すると
![]()
になります。
これを分散の式に代入すると
![]()
変形して
![]()
両辺の対数をとって
![]()
これで![]() について解くことができました。
について解くことができました。
次に
![]()
の両辺の対数をとって
![]()
移項して
![]()
![]() を代入して
を代入して
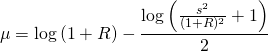
これで![]() について解くことができました。
について解くことができました。
まとめると![]() と
と![]() の関係は
の関係は
![]()
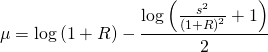
になります。
- リスク資産の複利確率(17)~シミュレーションのために連続複利年率を求める
- リスク資産の複利確率(18)~連続複利年率のリスクの求め方のはずが、どんでん返しに!
- リスク資産の複利確率(19)~シミュレーションのための連続複利年率とリスクの求め方とは?
リスク資産の複利と分布 期待リターンとリスクから分布を求める公式
「連続複利収益率をつかうと複数期間の計算が楽になる」と「連続複利収益率が正規分布するということ」を組み合わせると、リスク資産の複利について考えることができます。
「連続複利収益率をつかうと複数期間の計算が楽になる」では、![]() 年後の金額が
年後の金額が
![]()
になることを見ました。
「連続複利収益率が正規分布するということ」では、1年運用後の結果の分布が
![]()
になることを見ました。
これらを組み合わせると![]() 年後の結果の分布は
年後の結果の分布は
![]()
になります。
正規分布![]() の
の![]() 倍というのは、独立な正規分布
倍というのは、独立な正規分布![]() を
を![]() 回足し合せた分布です。
回足し合せた分布です。
「独立な正規分布」というのは、1年目と2年目のリターンに相関がないといったことことを言い換えたものです。
正規分布を足し合せた結果、すなわち、正規分布の和は、正規分布に従い、その平均は元の分布の平均の和、分散も元の分布の和となることが知られています。考えてはいけません。そういうことなのです。
つまり、![]() を正規分布
を正規分布![]() に従う確率変数、
に従う確率変数、![]() を正規分布
を正規分布![]() に従う確率変数としたとき、確率変数
に従う確率変数としたとき、確率変数![]() は正規分布
は正規分布![]() に従うということです。
に従うということです。
これより、正規分布![]() の
の![]() 倍は正規分布
倍は正規分布
![]()
に従うということになります。
これで、リスク資産の期待リターンとリスクの年率から、![]() 年後の運用結果の分布を求めることができるようになりました。
年後の運用結果の分布を求めることができるようになりました。
大事な公式なので、再度まとめておきます。
元本![]() 円、リスク資産の年率の期待リターン
円、リスク資産の年率の期待リターン![]() %・リスク
%・リスク![]() %(分散は
%(分散は![]() )を
)を![]() 年間運用した結果の分布は
年間運用した結果の分布は
![]()
ここで、
![]()
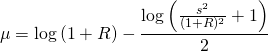
- リスク資産の複利確率(20)~シミュレーションの作り直し3度目の正直
- リスク資産の複利確率(21)~新しいシミュレーションを試してみる
- リスク資産の複利確率(22)~最も重要な公式、N年後の確率分布を求める式を記す
表計算ソフトでの計算方法とグラフの描き方
Excelなどの表計算ソフトを使うと、対数正規分布![]() の確率密度や、累積確率を簡単に求めることができます。
の確率密度や、累積確率を簡単に求めることができます。
対数正規分布の関数はLOGNORM.DIST(x, 平均, 標準偏差, 関数形式)です。
xには、求める確率密度(累積確率)の対象を設定します。例えば、リターンが10%の確率密度(累積確率)を求めたければ1.1と入力します。
平均には、対数正規分布のパラメタの平均、すなわち、連続複利収益率![]() の平均を入力します。
の平均を入力します。![]() 年後の分布であれば
年後の分布であれば![]() になります。
になります。
標準偏差には、対数正規分布のパラメタの標準偏差を入力します。![]() 年後の分布であれば
年後の分布であれば![]() になります。
になります。
これまでの議論では、分散で扱っていましたが、Excelでは標準偏差なので分散![]() の平方根をとって
の平方根をとって![]() になっていることにご注意下さい。
になっていることにご注意下さい。
関数形式には、求める値が、確率密度なのか、累積確率なのかを指定します。FALSEを指定すると確率密度、TRUEを指定すると累積確率になります。
xの値を変えながら計算してグラフにすると分布を見ることができます。
累積確率のグラフを書くと、だいたいどのくらいの確率でいくらになるかを見ることができますが、厳密に計算したい場合は、対数正規分布の累積確率の逆関数LOGNORM.INV(y, 平均, 標準偏差)で計算できます。累積確率の逆関数というのは、累積確率のグラフの縦軸(つまり確率)の値を指定して、対応する横軸の値(つまり金額)を求める関数です。
yには、求める確率を設定します。平均、分散はLOGNORM.DISTと同様です。
例えば、yに0.3を指定すると、指定したパラメタにおける、悪いほうから30%の確率の運用結果を求めることができます。
おわりに、ではなく、これがはじまり
ふー、長くなりました。ちょっと難しかったですかね。
腰を落ち着けてイーノさんの連載をよみながら、あれ?とおもったところのヒントがないかを探しに来ていただく、という読み方がよいかもしれません。
この記事では、連続複利収益率が正規分布正規分布する、という金融工学の考え方をもとに、リスク資産の期待リターンとリスクから、任意の期間後の運用結果の分布を求める式を手に入れることができました。
また、この分布が対数正規分布に従うことも理解できました。
今回の記事ではこの公式にたどり着くだけで精いっぱいでしたが、これがおわりではなく、これがはじまりだと考えています。
これらを活用すると、長期運用を続けていくにあたってぶち当たる、様々な疑問にこたえることができるからです。
これから、数回に分けて、以下のような気になる話題について考えていきたいと思います。
このために久しぶりにカテゴリも新設しましたよ!
- リスクがリターンを蝕むってどういうときにおこる?
- どういうリスクとリターンのバランスなら長期投資に向いている?
- 長期投資でリスクは減るの?増えるの?
- ウォール街のランダムウォーカーのバートン・マルキールさん曰く「長期投資でリスクは減る」
- 山崎元さん曰く「長期投資でリスクは減らない。バートン・マルキールの説明は間違いなのだ」
- 水瀬ケンイチさん曰く「「長期投資でリスクは縮小する」も正しいし、「長期投資でリスクは拡大する」も正しい。」
こうご期待!