長期投資でリスクは下がるのか下がらないのか。
今までの自分は「こっちが正しい!」もしくは「どっちも正しい!」を自信をもって判断することができずスッキリできていませんでした。
でも、前回のリスクはリターンの敵 – リスクとリターンと複利の関係の記事で得た前提と知識をもとにすれば、今度こそちゃんと理解できるはず…。
前回の記事で得た、前提と知識をもとにして、たびたび議論になるこの話題について、改めて確認してみることにします。
「長期投資はリスクを下げる」by バートン・マルキール「いや、それは間違いだ」 by 山崎元・・・どういうこと?
長期投資はリスクを下げるのか下げないのかの議論は、私にとっては古くて新しい問題。
というのも、バートン・マルキールさんは、2011年出版のウォール街のランダム・ウォーカー <原著第10版>―株式投資の不滅の真理の「リスクは投資期間に依存する」という節にて以下のように書いています。
株式投資のリスクも投資期間に応じて減少するのだろうか。答えはもちろん「イエス」である。株式を「長期間」保有し、一度買ったら多少の価格変動があっても我慢して持ち続けるという基本方針を貫けば、リスクの全部ではないがかなりの部分を減らすことができる。
他方、山崎元さんは、その著作や論説で一貫して「【長期投資はリスクを縮小させる】は間違い」としています。
マルキールの議論の誤りは、投資期間が異なる運用のリスクを「年率の平均リターンのちらばり方」で見ようとした点にある。
まず、「長期投資はリスクを縮小させる」は間違いです。
あたりまえですが運用期間が長期化するほど、運用資産額がとり得る上下の幅は拡大し、投資家にとっての不確実性は拡大します(その代わり期待収益も増えます)。
通常、運用期間の長さにつれて資産額の期待値もリスクも、ともに拡大します。
このように両者の言い分は平行線のようです。どちらかが間違っているのか、それとも両方あっているのか、自分の中ではっきりとした考えを持つことができていません。
でも、前回のリスクはリターンの敵 – リスクとリターンと複利の関係の記事で得た前提と知識をもとにすれば、今度こそちゃんと理解できるはず…。
前回の記事で得た、前提と知識をもとにして、たびたび議論になるこの話題について、改めて確認してみることにします。
投資における「リターン」と「リスク」という言葉の一般的な定義のおさらい
まず初めに、大前提となる、投資における「リターン」と「リスク」という言葉の一般的な定義についておさらいします。
投資信託協会の解説には
【リターンとは?】
投資を行うことで得られる収益のことです。【リスクとは?】
「結果が不確実であること」を意味します。具体的には、リターン(収益)の振れ幅のことを指します。
とあります。その他、各金融機関等が用意しているコンテンツでも、ほぼ同様の説明があります。実際、私の身の回りでも、この意味で使われることが一般的であり、コンセンサスの取れている定義といって問題ないでしょう。
また、1年を超える期間のリターンとリスクは、年率に換算して表示されるのが一般的です(参考:投資パフォーマンス基準 : グローバル投資パフォーマンス基準 | 日本証券アナリスト協会によるガイドライン)。
なお、リスクの年率換算は「事後的な標準偏差(月次リターンを使用)」とされています。
月次リターンから、3年間の事後的な年率換算リスク(標準偏差)を求める方法は以下の通りです。
- 対象期間の36個の月次リターンから、1か月単位の分散
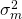 を求める
を求める - これに12をかけて年間の分散に換算(ちらばり方の一様な1か月単位の分散が12ヶ月継続することにより年間の分散とする)。1年間の分散は
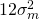 となる。
となる。 - リスク(標準偏差)は分散の平方根を取ったものなので、年率換算したリスク(標準偏差)は
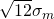
初出時、1か月単位のリスクに![]() をかけるとしていました。1か月のリターンを1年(つまり12ヶ月)に換算するので
をかけるとしていました。1か月のリターンを1年(つまり12ヶ月)に換算するので![]() が正しいです。インデックス・ドライバーのRockyさんよりご指摘いただきました。お詫びして、訂正いたします。
が正しいです。インデックス・ドライバーのRockyさんよりご指摘いただきました。お詫びして、訂正いたします。
リターンとリスクと複利の関係のおさらい
つぎに、前回の記事リスクはリターンの敵 – リスクとリターンと複利の関係の内容のおさらいです。
前回の記事では、連続複利収益率が正規分布するという前提のもと、リスク資産の期待リターンとリスクの年率から、![]() 年後の運用結果の分布を求めることができるようになりました。
年後の運用結果の分布を求めることができるようになりました。
その公式は以下の通りです。
元本![]() 円、リスク資産の年率の期待リターン
円、リスク資産の年率の期待リターン![]() %・リスク
%・リスク![]() %(分散は
%(分散は![]() )を
)を![]() 年間運用した結果の分布は
年間運用した結果の分布は
![]()
ここで、![]() は対数正規分布。
は対数正規分布。
![]()
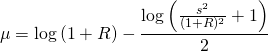
この式から、![]() 年間の運用によるリターンの分布は
年間の運用によるリターンの分布は![]() となることがわかります(運用後の金額を元本で割る。リターン0%が1となることに注意)。
となることがわかります(運用後の金額を元本で割る。リターン0%が1となることに注意)。
長期投資でリスクは減るのか?
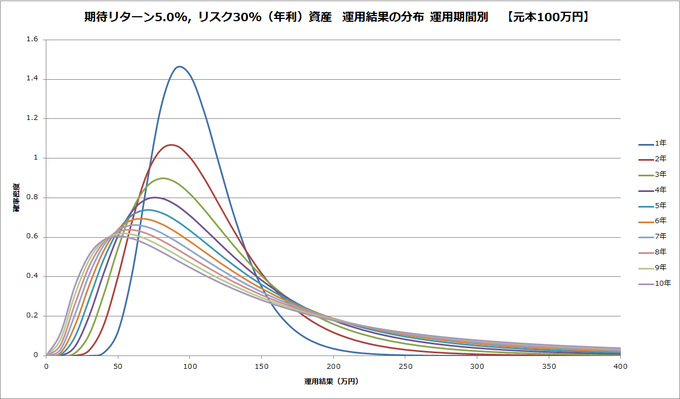
まずグラフから傾向を確認します。前回、元本100万円を、期待リターン5%、リスク30%(いずれも年率)の資産を1, 2,…,10年と運用していった場合の運用結果のグラフを描きました。
運用期間が長くなるにつれ運用結果の分布が広くなることがわかります。
このグラフの横軸は運用結果ですが、元本100万円でわると、n年間のリターンになります。つまり、運用期間が長くなると、リターンの分布が広がりそうだということがわかります。
このことを数式で確認してみます。
![]() 年間の運用によるリターンの分布は
年間の運用によるリターンの分布は![]() です。
です。
対数正規分布の特徴から
![]()
の分散は
![]()
になります。
これらより、
![]()
の分散は
![]()
となります。これこそが、![]() 年間運用した結果のリターンの分散=振れ幅(年率換算前)です。
年間運用した結果のリターンの分散=振れ幅(年率換算前)です。
運用期間が長くなる、すなわち、![]() が大きくなると、これがどうなるかを見てみます。
が大きくなると、これがどうなるかを見てみます。
![]()
つまり、年率換算前の分散は無限大に発散し、運用期間が長くなるにつれリスクは大きくなることがわかります。
次に、期間内のリターンの振れ幅が一様という仮定のもと、年率換算のリスク=1年あたりのリターンのブレを確認します。とはいえ、連続複利率が正規分布するという前提のもとでは、
- 1年間のリターンの分布は
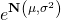
- これが対数正規分布
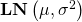 に従う
に従う - その分散は
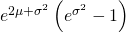
となり、年率換算のリスク=1年あたりのリターンのブレは![]() で、運用期間に依存しないことがわかります。
で、運用期間に依存しないことがわかります。
年率でみるとリスクは変わらないが、(運用は複利であるため)運用期間が長くなるにつれ、先に見たように全運用期間でのリスクは増して行くということです(これがまさにリターンとリスクと複利の関係)。
ここまで見た限りでは、「長期投資でリスクは増える=運用期間が長くなれば長くなるほど、最終的な運用成果のブレは大きくなる(年率換算リスクは一定だとしても)」といえそうです。
初出時、リスクの年率換算を、n年運用後のリターンの分散をnで割ることにより求めておりましたが、これは年率換算の方法としては適切ではありませんでした。インデックス・ドライバーのRockyさんよりご指摘いただきました。お詫びして、上記のように訂正いたします。
ウォール街のランダム・ウォーカーにある図の意味
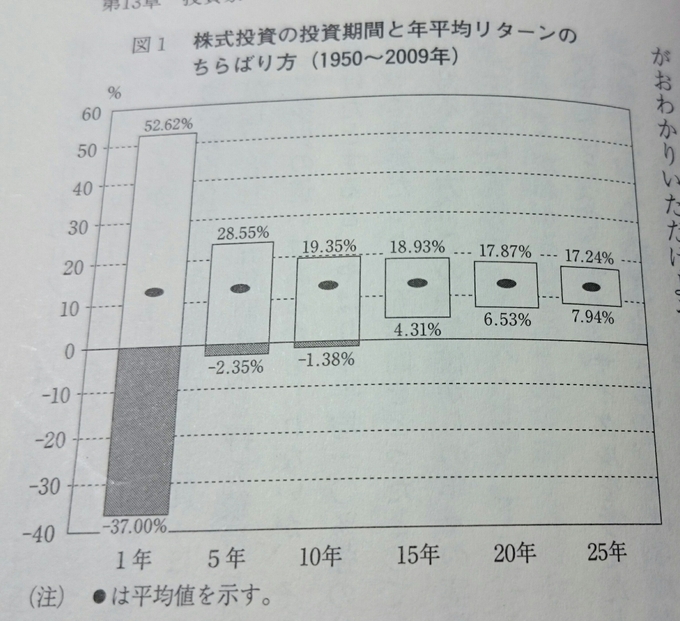
では、バートン・マルキールさんの言っていることが間違えているのか…。あらためて、ウォール街のランダム・ウォーカー <原著第10版>―株式投資の不滅の真理の「リスクは投資期間に依存する」の節の図1を確認してみます。
この図は、キャプションにもあるとおり「株式投資期間と年平均リターンのちらばり方」を表現した図です。
なるほど、これを見ると、投資期間(運用期間)が長くなるにつれ、「年平均リターンのちらばり方」は小さくなっています。これをもって「リスクは投資期間に依存する」「株式投資のリスクも投資期間に応じて減少する」としているようです。
ちなみに、このような図は他でもよく見かけます。
ここで「年平均リターンのちらばり方」が何を意味しているのかが気になってきます。すなわち、この図をどうやって書いたかということ。
何度も何度もこの節の文章を読み込み、元データとされているS&P500の1950年から2009年のデータを使って試してみてわかったのは
- 各年の年間リターンのデータを用意
- タップ数(サンプリング数)1, 5, 10, 15, 20, 25について移動平均を計算。
- タップ数毎に移動平均の、最小、最大、平均を求めグラフにプロット
を行っているということ。
移動平均というとわかりにくいかもしれませんが、過去n年間の、n個の年間リターンの平均を移動しながら繰り返し求めていく方法です。
具体的には、以下の図のように、オレンジ色の範囲内の複数の、1年間のリターンの平均を求めていきます。図は5年間の例なので、5つの年間リターンの平均を移動しながら計算していきます。
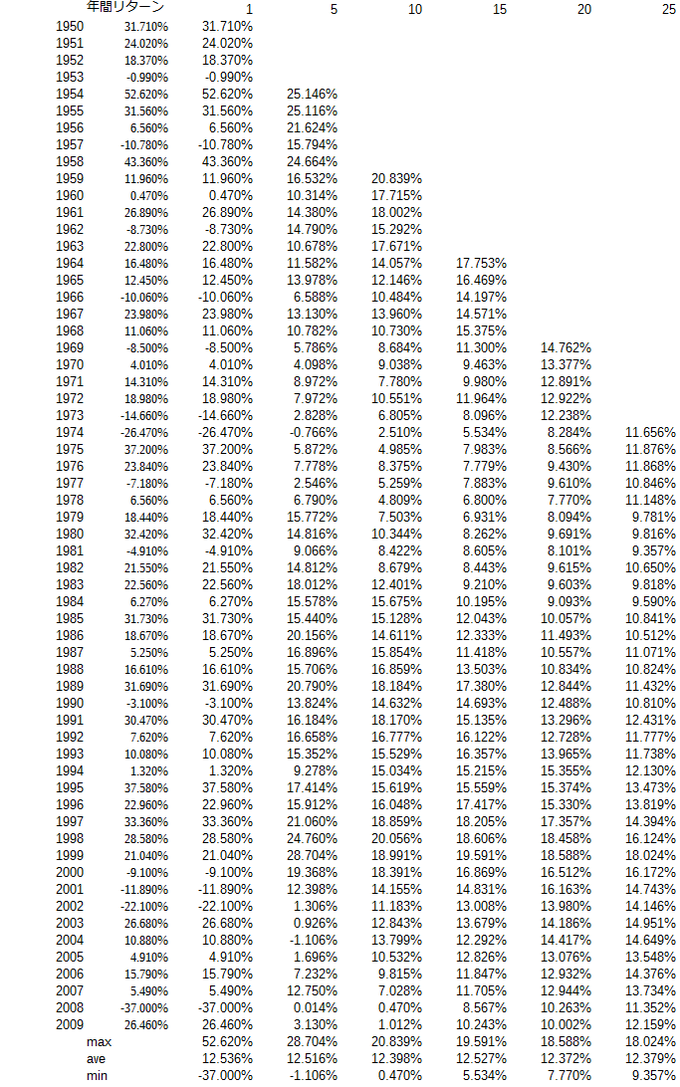
ためしに、検索でみつけたページにあった1950年-2009年のS&P500のトータルリターンと思われるデータを使って計算した結果は以下の通りです。
完全一致はしませんでしたが(元データは配当込みのようでその計算過程に違いがある可能性大)、大体似たような結果を得ましたので、図の書き方はこれであってそうです。
初出時1950年のリターンが計算に含まれていませんでした。お詫びして訂正いたします。
ここまで見ての感想としては、こうして求めた「投資期間別の年平均リターンのちらばり方」を「リスク」と呼ぶのはいささか無理があるかな、というが率直なところです。
年数=移動平均のタップ数(サンプル数)を増やせば、全体の平均(算術平均)への誤差が少なくなるということを言っているにすぎません。
少なくとも、それを「投資対象を保有し続けられる期間が長ければ長いほど、ポートフォリオに占める株式の割合を高めるべき」の根拠にするのは弱いのではと考えます。
上記の方法で求めた移動平均は、母集団から連続する一定数を抽出した「標本」の分布「標本分布」の平均を求めたもので「標本平均」になります。
「標本分布」の標準偏差は「標準誤差」です。
「標準誤差」は「標本」の数の平方根に反比例することが知られています。
こう書くとややこしいですが、標本の数を増やせば、誤差が少なくなり本当の平均(母集団の平均)に近づいていくということです。標準誤差は母集団の平均の区間推定をしたい場合などに重宝します。
今回のケースの場合、移動平均の期間=対象年数を長くすれば、本当の平均(母集団の平均)に近づいていくということを言っているわけです。
しかも、ここでの「平均」は「算術平均(総和をデータ数で割る)」であって運用期間とリターンの関係を語るには適切とはいえません。同じ平均10%でも、「毎年10%」と「30%, -20%の繰り返し」では結果が全然変わってきます。
インデックス・ドライバーさんの記事(リスクは投資期間に依存する・・・?|インデックス・ドライバー)でもほぼ同様の結論のようでした。
これをもって、節のタイトルは「リスクは投資期間に依存する」となっています。しかしながらこの言葉はミスリードで、これが言わんとしていることは、
「1ヶ月でも1年でも10年でも期間に関係なくそれらを1回の投資とするならば、その1回の投資におけるリターンのバラツキ(これをリスクと言っている)は期間が長いほど小さくなる」
ということだと思われます。
要は移動平均というローパスフィルタをかけて解像度を落としているだけです。
決して、
「投資対象そのもののリスク(毎月のリターンのバラツキ)が低下するわけではない」
ということに注意が必要です。
おわりに
あくまで、「連続複利収益率が正規分布する」という仮定の下でのシミュレーションではありますが、ここまで見てきて、ようやくスッキリしました。
一般的な「リスク」という言葉の定義の下では「長期投資でリスクは下がらない」が正しそう。リターンとリスクと複利の関係を踏まえるとリスクは時間とともに増えていく。
「リスク」を「標準誤差」の意味でつかっているのであれば確かに「長期投資でリスク(標準誤差)は下がる」は正しい。
しかし、それを「投資対象を保有し続けられる期間が長ければ長いほど、ポートフォリオに占める株式の割合を高めるべき」の根拠にするのはちょっと飛躍しすぎかな。
という理解です。
いつになるかまだわかりませんが、次回はリスクとリターンの関係「どういうリスクとリターンのバランスなら長期投資に向いている?」について掘り下げてみてみることにします。




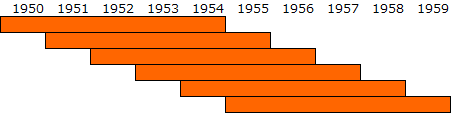


コメント
森村さま
インデックスドライバーのRockyです。お世話になっております。記事の引用ありがとうございます(^^)
細かい話で恐縮ですが二点ほど気になった点があります。行き違いでしたらご容赦願います。
①標準偏差の年率換算(『投資における「リターン」と「リスク」という言葉の一般的な定義のおさらい』の項)
データは36ヶ月分使うと思いますがあくまで年率(12ヶ月)換算なので「×√12」でよいのではないでしょうか?あるいは「(1+σ/√12)^12」とするとより発散が速いと思います。
②対数正規分布の分散の年率換算(『長期投資でリスクは減るのか?』の項)
年率換算として「/n」をされていますが、複利(積)なので「^(1/n)」のような気がするのですがどちらを適用するのがよいのでしょうか?
ある決まったバラツキの累積ならば、それを年率に割り戻したら直感的にはnに依存せず元の定数になると思うのです(この場合は極限で分散が「e^[2(μ+σ^2)]」に収束。つまり長期投資でリスクは不変)。相加平均と相乗平均の関係に近いと思います。考え方、あるいは定義の違いだけかも知れませんが・・・。
以上、ご検討よろしくお願い致します。
ありがとうございます。
1点目は、まさにその通りでした。36ヶ月のデータから求めた1か月のリスクなので、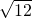 を乗じるべきところでした。GIPSの文章には明示的な計算方法はみあたらなかったのですが、月次のデータから換算するとなるとやはりこの方法になるのでしょうね。
を乗じるべきところでした。GIPSの文章には明示的な計算方法はみあたらなかったのですが、月次のデータから換算するとなるとやはりこの方法になるのでしょうね。
2点目については、かなり迷って複利で発生した分散を算術平均的アプローチで年単位に換算していました(あえてマルキールの図の土俵にそろえる=複利の運用を算術平均で語る)が、ご指摘のように正確ではありませんでした。年単位でのリスクは一定だが、そのリスクが積み重なっていくことにより全体のリスクは上がっていくと段階をふみながら進めるべきところでした。
いずれも、経緯を残したうえで、訂正いたしました。改めまして、ありがとうございます。今後ともよろしくお願いいたします。
PS1.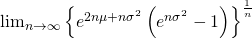 の証明が自分のへっぽこ数学ではきれいに求めることができず、単年のリターン分布に戻って年率換算リスクを
の証明が自分のへっぽこ数学ではきれいに求めることができず、単年のリターン分布に戻って年率換算リスクを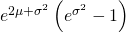 として逃げてしまいました…。無念。
として逃げてしまいました…。無念。
“[latex]LaTex記法[/latex]”で数式が記載できるようになっております。
森村さま
Rockyです。
>あえてマルキールの図の土俵にそろえる=複利の運用を算術平均で語る
この本有名な割にあまり良くないんですよね。
>証明が自分のへっぽこ数学ではきれいに求めることができず、
私も特別なことはしておらずエクスポネンシャル(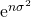 )に対して1は無視できるということで落としているだけです。
)に対して1は無視できるということで落としているだけです。
あと差し支えなければブログでテフを使えるようにする方法を教えていただけないでしょうか?
以上、よろしくお願い致します。
何とかして、「はさみうち」にできないかと頑張ってみましたが発散速度から自明なこととして変形しちゃえばよかったんですね。
このブログは、Wordpressをつかっているので、WP QuickLatexというプラグインを入れることにより、LaTeXで式が書けるようになります。
http://valavg.com/running-blog-with-wordpress/
一般的なブログサービスだと難しいかもしれません…。Rockyさんのブログだと、LaTeXが使えれば重宝しますよね。
森村さま
Rockyです。ありがとうございます。やはりそれなりのシステムを用意しないと厳しいということですね。
長期投資による標準偏差の変化について検索していてたどりつきました。
興味深いデータありがとうございます。
S&P500のデータとグラフですが、リターンの算術平均ではなく5年リターンの5乗根を取ると、ぴったり同じ結果になりました(なぜか5年と10年の最小だけが一致しませんが)。Google Spreadsheet化したものがこちらです。
https://docs.google.com/spreadsheets/d/1N40MY1Zv5vkk-RJ46D54URSKxdTOGZwOAE5vFvYhPdA/edit?usp=sharing
1949年末の株価を100として、そこから毎年のリターンを元に年末の株価を算出しています。その後、5年間隔の株価変動率を年換算しています。詳しくは、表の中の数式を見てください。
貴重な情報ありがとうございます!算術平均ではなくて幾何平均のばらつきの最小、平均、最高だったんですね。
幾何平均だったとしてもやはり、強引な結論だなという点には変わりなさそうですね。
後日、記事のほうに追記させていただきます。
幾何平均とも違うと思います。30%と15%に対して、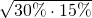 のようにするわけではないので…。
のようにするわけではないので…。
マルキール氏は、「リスクとは、リターンの年率のバラつき(標準偏差はバラつきの指標の1つ)のことである」と定義しているようなので、S&P500のデータをもとに「長期になればリスクは縮小する」と主張するのは正しく思えます。
「その定義だと、一般的に”リスク”という言葉で感じる感覚とは違いますよね」というのが山崎氏の主張。
下記の記事が、この2つをグラフで説明していると思います。
http://randomwalker.blog19.fc2.com/blog-entry-1996.html
ありがとうございます。
ご紹介いただいた梅屋敷商店街のランダム・ウォーカーさんの記事は、私も把握しておりました(この連載の前回の記事でリンクしておりました)。
いただいたシートを拝見して、私が「移動算術平均ベース」で計算してたのが、正しくは「移動幾何平均ベース」だったのかと得心してい次第ですが、手元でいろいろ確認できる環境に戻ったら再度じっくり自分で確認してみます。
マルキールさんの前提としている定義と、それに対する山崎さんの指摘については、柳田さんと同じ理解でいるつもりです。
そして、記事本文に記載した通り、マルキールさんのリスクの定義と、そこからの主張は一般的ではなく飛躍があるなぁ、というのが私の理解です。
山崎さんにしても、梅屋敷さんはじめブロガーにしても誰も「ウォール街のランダムウォーカー」を正しく理解していない事に悲しくなりますね・・・。
効率的市場仮説の肝とは、「現在のファンダメンタル」と「将来への期待」を常に株価が反映しているという事であって、数学的な意味合いではないですよね。
純数学的にいうと山崎さんやこのエントリが正しいと思いますが、歴史的にみると大間違いです。なぜなら世界経済は常に成長を続けているし、それを株価が反映してるからです。また、マクロ経済には常に中央銀行と政府の手が加えられてて、経済成長率というのは、全くのランダムではなく人為的な影響を多分に受けているからです。
長期投資すればリスクが小さくなると言う事は、長期的に見れば経済成長を株価が反映すると言うことです。(先進国の経済成長率は毎年数十%も変動しない。マルキール教授は経済学教授)
コメントありがとうございます。
ただおっしゃっている内容を私はよく理解することができませんでした…
純数学的なのか歴史的なのかや、効率的市場仮説、経済成長率についてはなにも言及しておりません。
是非ご自身のブログなどで、悲しいと思われている思いの丈など論を展開なさってみてはいかがでしょうか?
はじめまして,cartman と申します。
ファイナンス関係を勉強中の者です。
「リスクは時間の長さの平方根に比例する」関係の情報を調べていて行き着きました。
個人的に、例えば5年保有するもので5年間のリスク(標準偏差)を計算した際に、
そのリスクを年率換算すること自体がナンセンスだと考えているのですが、どうでしょうか。
「5年間のリスクを年率換算したもの」が意味を持つケースは、
4年保有した時点でのリターン(収益率)から残り1年のリスクはどのくらいかを計算する場合には意味を持つような気がしていますが、どうでしょうか。
見当はずれな質問であれば、すみません。。
コメントありがとうございます。
はい。その通りだと思います。本記事中複数年運用後のリスクを、あえて年率換算しようとしたのは「長期投資でリスクは低減する」という主張に「年率にならせばリスクは減る」という説明がついてまわることがよくあるように感じられたからです。
当方の現在の結論に関する理解ははこの記事の「おわりに」の節、およびコメント欄にてRockyさんとやり取りした通りです(長期投資でリスクは低減する vs 低減しないの議論は、「リスク」の定義が異なっているから。集計期間が長くなれば標準誤差が減るのは当たり前。期間に寄らず、もともとの資産のリスクは一定だが、運用期間が長くなれば投資成果のばらつきは広がっていく)。