これまでの検討で、バリュー平均法のしくみをだいぶ理解することができました。それと同時に実践するにあたり課題となる点も明らかになってきました。バリュー平均法の良いところをそのまま活かしつつ、問題点を抑制した修正バリュー平均法（変形バリュー平均法）を検討・検証してみます。
バリュー平均法の問題点
これまでに分かっているバリュー平均法の主な問題点をおさらいしておきます。詳細については別途該当記事をご参照ください（末尾に関連記事としてリンクしてあります）。
- 毎期の積み立て金額の調整額が、保有リスク資産額に比例する。
- マーケットが継続的に上昇する場合、リスク資産の比率を下げるため、その先の上昇に対して機会損失となる。
- 金融期間に一度積み立て設定すればあとはほったらかしでよいコスト平均法と比べると、手間がかかる。
一つめの「積み立て調整額が保有リスク資産額に比例している」点が、バリュー平均法を実践していく上で様々な問題をひきおこしています。
今回はこの点に集中した修正バリュー平均法を検討します。
世には、様々な積み立て投資の方法がありますが、それぞれの方法の差は、つきつめれば、「各期にどれだけの額を投資するか」を決定するためのアルゴリズムの違いに集約できます。
バリュー平均法の場合、このアルゴリズムを、
と表現することができます。
は毎期の基本積み立て金額つまり毎期の基本バリュー増分、
は積み立て金額の増加・減少を切り替えるための閾値となる期待リターン、
は直近のリターン実績、 
は前回積み立て後のリスク資産評価額です。
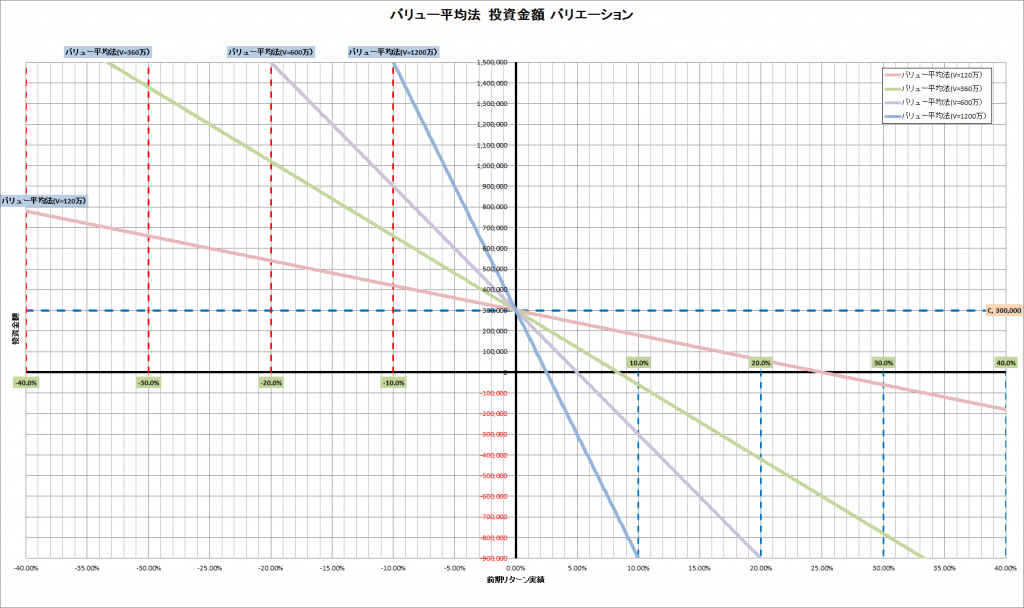
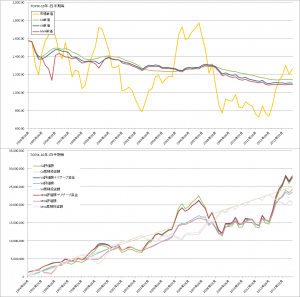
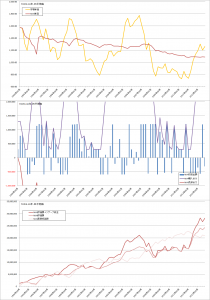
グラフをつかって具体的な金額を見るとこの問題の大きさがよくわかります。
このグラフは、が120万円、360万円、600万円、1200万円それぞれについて、の変動による積み立て金額の変化を示したものです。は30万円としています。ここではみやすさ考慮し、は0としています。を設定するとグラフが、増加方向にそのまま平行移動します。
平常時のリターン実績の目安として、3ヶ月で±20%程度の変動は普通にあるものととらえておくのがよさそうです。また、暴落レベルの場合、3ヶ月で40-50%の下落、その前後にも20-30%の下落は想定しておく必要があります。たとえば、リーマンショックでは、2008年8月→2008年11月の3ヶ月で、MSCI-AWCI（円換算）は約43%、MSCI-KOKUSAI（円換算）は約34%、TOPIXは約33%下落しています。その前後にも20%前後の下落がみられます。
保有資産が大きくなるほど、グラフの傾きがきつくなり、マーケットの変動がわずかでも大きな金額の売買が必要になることがわかります。
これにより引き起こされる投資パフォーマンス上の問題は以下の通りです。
- 大幅な下落時は資金が枯渇してしまう
- 最初の下落時に集中投資となってしまい、その後さらに下落した場合傷が深くなる
- 課税口座での運用の場合、売却益に対する課税も無視できない（含み損の状態でも売却が発生することがあることに注意。その場合は税金がかからない＆損益通算可能）
- 逆に積み立て開始直後は調整額が小さくなり効果が小さくなる
また、メンタル的負荷も無視できません。
- 資産が増えると毎期大金を動かすことになり精神衛生上好ましくない
- 現実的な投資額に抑えるために何らかの独自ルールを策定する必要があり主観が入る余地が生まれ結果に対する後悔の念を排除できない
バリュー平均法のよいところ
バリュー平均法では、直近のリターン実績に基づき、一種のリスク資産と無リスク資産間リバランスを行っています。リバランスの効果として、リスク資産の運用効率＝リターンを（コスト平均法による積み立てと比較して）高くすることができます。
リスク資産と無リスク資産の比率を一定に保つ単純なリバランスよりも投資効率が高い（待機資金の金額が同額程度の定率リバランス法より投資効率が高い）ことからも、直近のリターン実績に基づくリバランスは一定の効果が認められるといってよいでしょう。
修正バリュー平均法の方針
直近のリターン実績に基づき積み立て額を調整する点は活かしつつ、調整額の決定アルゴリズムを変更してみます。
具体的には、基本積み立て金額とリターン実績をもとに調整額を決めるようにします。
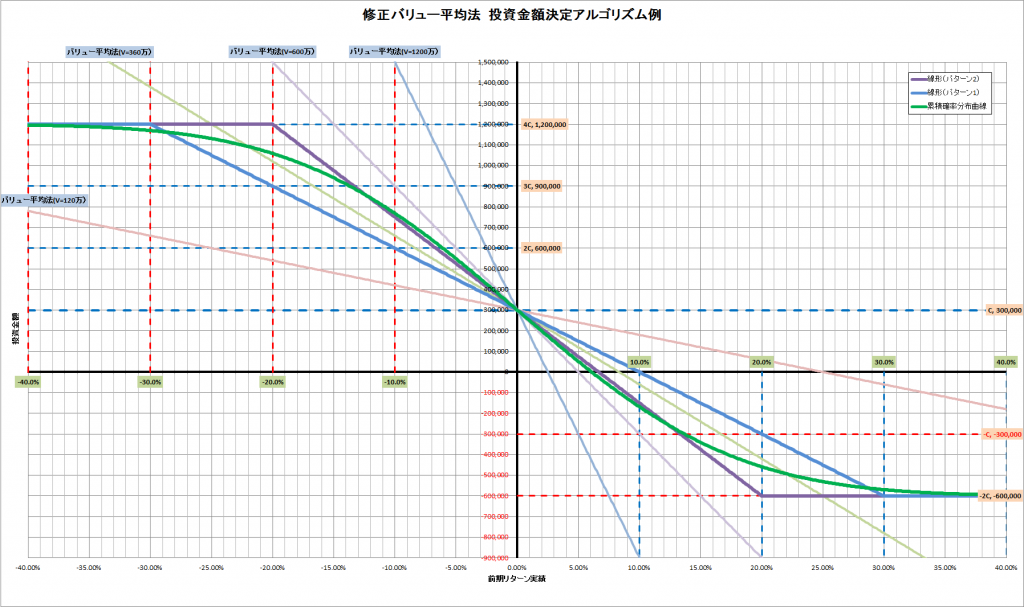
このグラフで示した例のようにいろいろやり方はあります。自分の考え方に一番近く、しっくりきて心地の良いルールを選ぶのがよいでしょう。
直線でも曲線でも、段階的な離散値でもかまいません。
今回は私の現時点での直観に近い累積確率分布曲線をつかってみます。
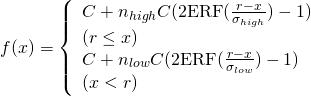
関数
は、正規分布に基づく累積確率分布曲線ないしガウスの誤差関数とよばれる関数です。正規分布を0からまで積分（足し込み）した値です。上記の式は
、
、
を前提とした式です。
EXCELにもERF関数が用意されていますが、
、
、になっているので注意が必要です。
曲線の形を制御する定数パラメタとして、調整額のへの倍率
、 傾きを制御する
が設定可能です。直近のリターン実績が期待リターンより高いときと低いときで結果を切り替えるために、highとlowの2通りのパラメタを設定できるようにします。ただし、以下の検証ではhigh, lowでパラメタは同じにしています。
バックテスト
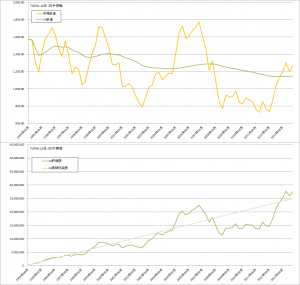
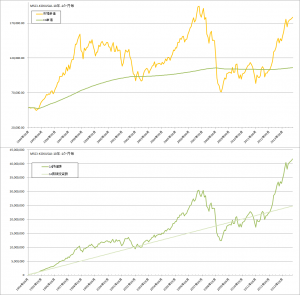
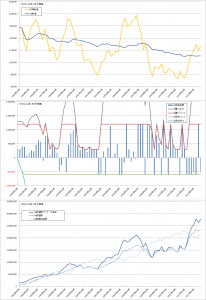
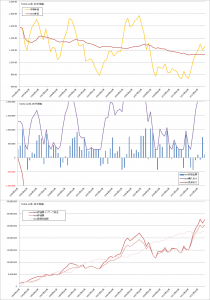
前回と同じように、過去10年間のMSCI-KOKUSAI（円換算）、TOPIXの実績をつかって、コスト平均法、バリュー平均法、修正バリュー平均法のバックテストをおこなってみます。
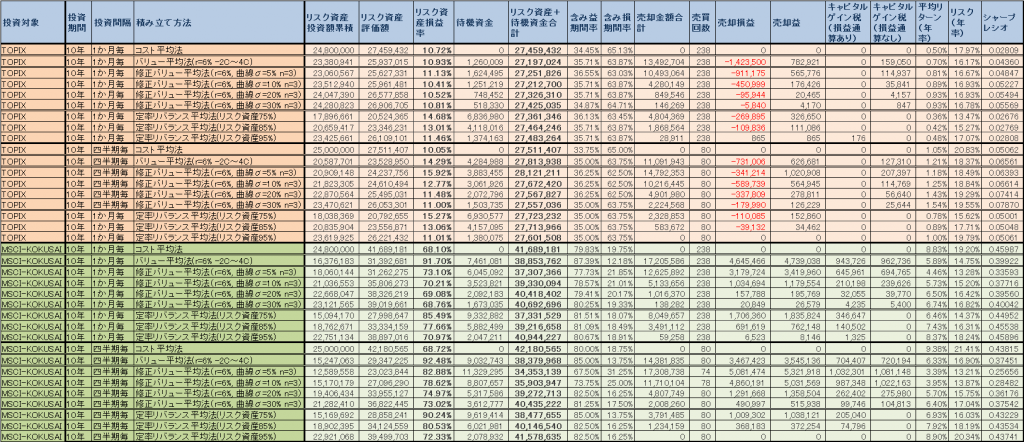
コスト平均法・バリュー平均法・修正バリュー平均法の比較
- 修正バリュー平均法は、ねらい通りコスト平均法と比較して、高い投資効率を維持できている。
- 投資金額の変化がバリュー平均法よりはマイルドになっており、ちょうどコスト平均法とバリュー平均法のあいだくらいの成績・挙動になっている。
- 待機資金に資産をキープしているため、最後に大幅に上昇している今回のテストでは機会損失となっている。資産総額ではフルインベストメント状態のコスト平均法の成績がよい。
- 曲線のσが小さい＝傾きが大きい＝調整額の変動が大きいほうが、効率が良く、ポートフォリオ全体のリスクも低い。リバランスの割合が大きいことがこのテストケースではいい方向に働いている。
が特に気づいた点です。
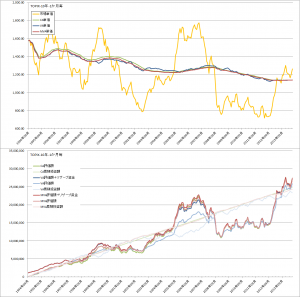
次にグラフで見てみます。
グラフのパラメタは
- 3ヶ月に一回の積み立て
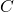- は30万円
- は6%
- バリュー平均法は、購入は最大4C=120万円まで、売却は最大2C=60万円までに制限。
- 修正バリュー平均法の曲線のσは20%、高値・安値とも倍率3。つまり、購入は最大4C=120万円まで、売却は最大2C=60万円まで。
としています。
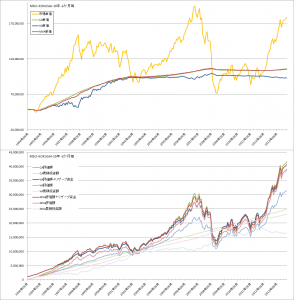
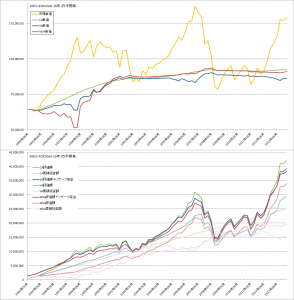
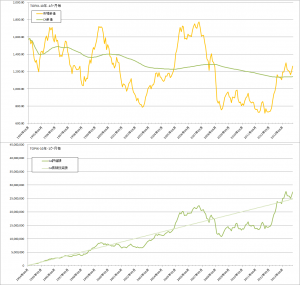
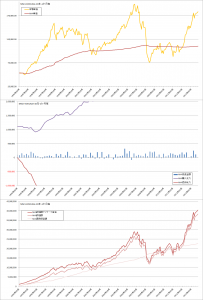
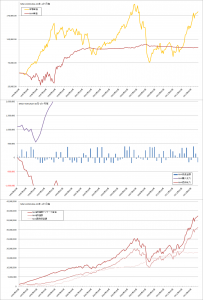
TOPIXでの比較
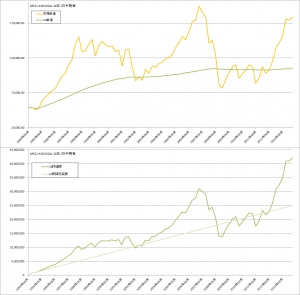
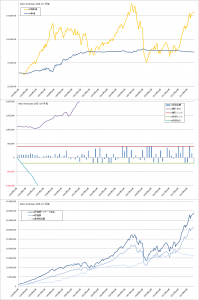
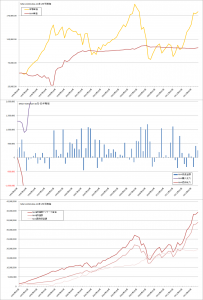
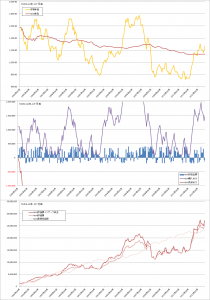
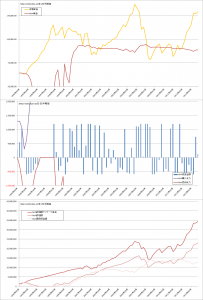
MSCI-KOKUSAIでの比較
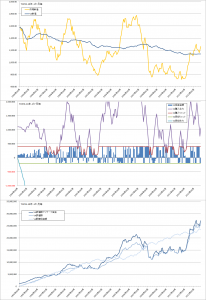
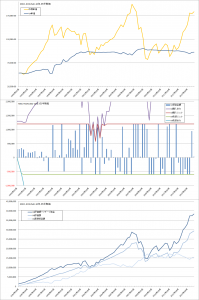
つぎに各方法の詳細です。
コスト平均法
バリュー平均法
修正バリュー平均法
曲線σ=20%の場合
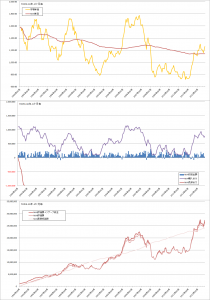
曲線σ=5%の場合
考察
修正バリュー平均法は、バリュー平均法の特徴を引き継ぎつつ、投資額の変動を少しマイルドにしたもので、結果を見る限りねらいどおりに働いているようです。ちょうどバリュー平均法とコスト平均法のあいだくらいの成績・挙動になっています。
少なくとも通常のバリュー平均法のアルゴリズムで出力された調整額を上限、下限でクリップするより、別途、調整額決定ルールを決めるほうが合理的といえるでしょう。今回のようにマイルドにしたり、逆にバリュー平均法よりさらにダイナミックに変えるなど、あらゆる投資家の意思を反映させることが可能です。バリュー平均法のルールは数多くあるルールのなかの一例に過ぎないということもできます。
他方、調整額が資産総額と無関係の修正バリュー平均法では、リスク資産の規模が増えていくにつれ、調整額による調整の影響が希薄化していっています。期間全体を通して、ルールで効果をキープするためには、ある程度資産規模を加味せざるをえないということもわかります。
今回の結果でも、バリュー平均法・修正バリュー平均法の待機資金を持つことによる機会損失が気になります。今回のバックテスト対象のTOPIX、MSCI-KOKUSAIとも、最後に大きく上昇しているためその影響が顕著に表れています。
「将来は不確実でリスクがあるとしても、リターンは有利だと思って投資する」という理由で投資するのだから、その時点時点で、投資家が自分にとって最適だと思う金額を投資している状態が意志決定としてはベストなのであり、ドルコスト平均法によって、この状態の達成が遅れるなら、その間の投資金額不足は、機会損失として理解すべきだ。
バリュー平均法の実践のためには、基本の積み立てルールとは別に、退避した待機資金のリスク資産への戻し方についていろいろ考える必要がありそうです。待機資金の量を調整額決定に盛り込むといったルール面での対応、投資家の責任での押し目買い（フォーミュラ投資の枠をどび出しますが）など。
いずれにしろ、調整額決定ルールに正解というものはないですし、すべてをルールでカバーしようとすることにも無理があります。目的はシステムトレードをするわけでも、新しい方式を発明してひともうけすることでもなく、ただ単に自分で納得した考え方に基づいて自身の資産形成をコツコツうまく進めることなのです。このことを忘れずに、今後も心安らかにコツコツ投資を継続できるよう勉強・検討を継続していきます。
おまけ：今後の検討ネタ帳
- バリュー平均法と定率リバランス法の考え方を組み合わせるとどうなるか
- バリュー平均法と修正バリュー平均法の、リスク資産：退避資金の割合の挙動
- 待機資金のリスク資産への戻し方
- 3ヶ月に一度の効率がよくなる根拠
- 過去の実績としてのマーケットの動き方
- 変化幅と変化にかかる時間の関係
追記（2014年8月4日）
改めて、バリュー平均法の原書（考案者による解説本）を開いてみると、バリュー平均法とコスト平均法の比較はもっぱらリターンの効率（損益率）で行っています。比較の表でも、資産総額ではコスト平均法のほうが多くなっています（そもそも、コスト平均法は毎期100ドル積み立て、バリュー平均法は毎期100ドルずつ資産評価額が増えるようバリューパスを設定しているので前提条件が異なる）。
資産総額での比較、待機資金を持つことによる機会損失に関する議論は見当たりませんでした。
大分記憶が薄まってきている＆以前よりは知識が増えていて、以前読んだときとはちがったった気づきがあるはずなのでそろそろ再読しなくては。
機会損失の件はバリュー平均法のFAQのはずなので海外のブログ記事などですでに議論されているかもしれません。